Hierarchical Low-Rank Approximation
Dense matrices appear in many computational applications such as boundary integral methods for solving homogeneous partial differential equations, kernel summation (convolution) problems in statistics and machine learning. Such dense matrices usually have structure within them, which can be used to compress them using hierarchical low-rank approximation. In doing so, the storage of the dense matrix reduces from O(N2) to O(N), while the O(N3) complexity of matrix multiplication and factorization becomes O(NlogpN). This is an extremely powerful tool when N is large.
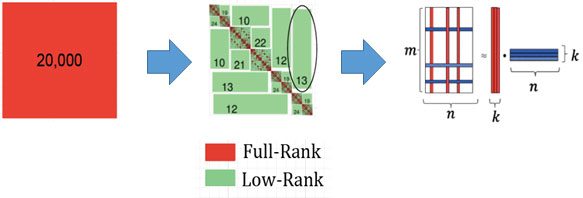
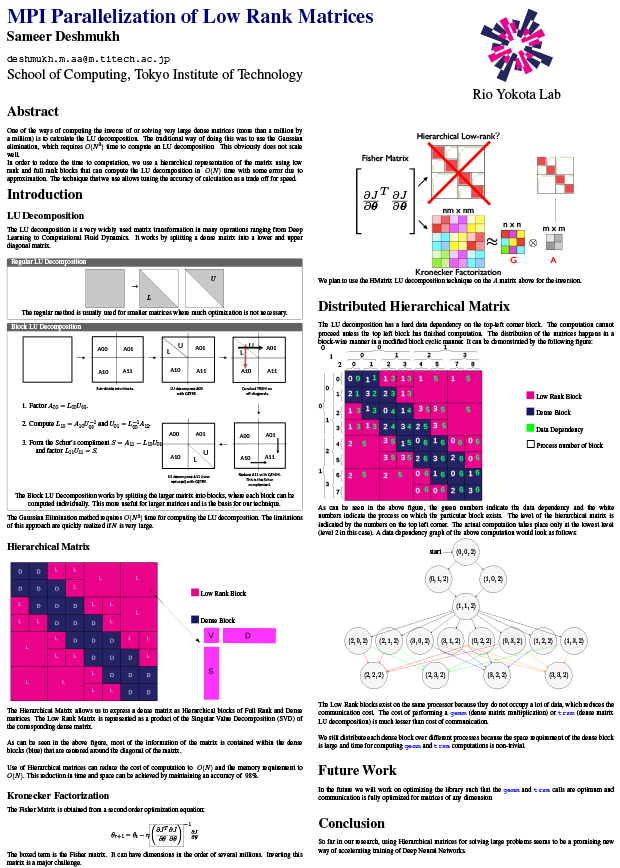
Figure 1 Compression of a Dense Matrix (red) Using Hierarchical Low-Rank Approximation (green)
Application to Deep Learning
Deep learning does not require very high precision, and this fact is exploited by the recent low-precision hardware from NVIDIA and Google. However, the matrix multiplication -- which is a dominant part of the calculation time in deep learning – is still done using dense matrices without any approximation. Even if the matrices themselves are full rank, proper reordering and blocking can reveal the underlying structure, which can then be used to perform low-rank approximations. This will reduce the storage from O(N2) to O(N), and the complexity of matrix multiplication from O(N3) to O(NlogpN).
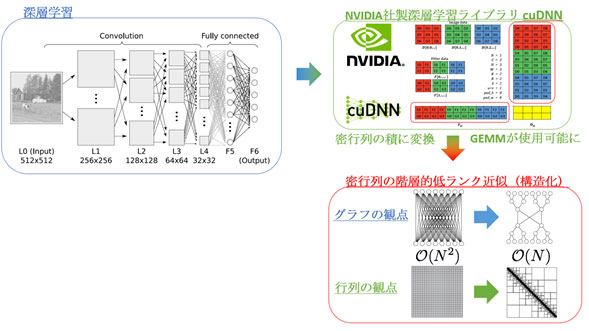
Figure 2 Accelerating Deep Learning Kernels with Low-Rank Approximation
MPI Parallelization of Low Rank Matrices
Introduction
Computing the LU decomposition of very large dense matrices (a few millions in dimension) is a very time-consuming task using traditional techniques like Gaussian elimination, which takes O(N3) time for reaching a solution. Approximating this dense matrix as a Hierarchical matrix can allow us to reduce the computation time to almost O(N) with an approximation error of about 98%.
Hierarchical Matrix
Hierarchical matrices consist of two kinds of matrix blocks - dense and low rank. The dense blocks are full rank matrix blocks that cannot be approximated without huge loss of information, and are therefore stored as-is in the matrix. The low rank blocks are off-diagonal blocks in the larger matrix that can be approximated using the SVD decomposition and maintain good enough accuracy for a well chosen rank.
Distributed Hierarchical Matrix
Large hierarchical matrices by themselves are very hard to fit on a single machine due to constrains of memory. Therefore, distributing them on multiple nodes and building a communication framework using MPI is very useful.
The distribution of the low rank blocks across processes determines how load balanced the final solution will be. We currently use a modified block cyclic distribution scheme where adjacent dense blocks are distributed on different processes whereas adjacent low rank blocks exist on the same process.
My current research area focuses on creating the most optimum distribution scheme for distributed hierarchical matrices such that the communication overhead for computing the LU decomposition is minimized.