Current Research Topics 2024
Pretraining Large Language Models (LLMs)
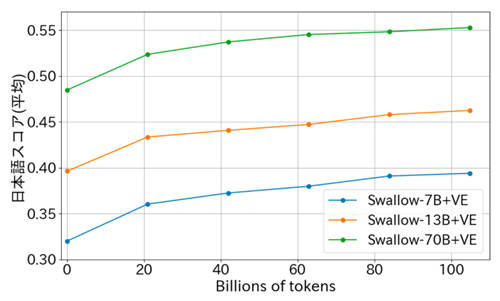
The Yokota Lab is developing a Japanese large language model Swallow in collaboration with the Okazaki Lab and AIST. Since pretraining from scratch requires a huge amount of computing resources, we have decided to perform continual training on Japanese text from open models such as Llama and Mistral, which were trained mainly in English. The model parameters are published on HuggingFace, so they can be used for research and commercial purposes. In contrast, the LLM-jp model developed at the NII LLM Research and Development Center is pre-trained from scratch in Japanese and English. In addition to the model parameters, we also plan to publish the data used for training and also the failed cases.
Pretraining Large Vision-Language Models Using Synthetic Images
In the past, we have conducted pre-training of the Vision Transformer using basic shapes such as fractals in place of real images in joint research with the Artificial Intelligence Research Center at AIST. However, since it is important to link real-world images and language in image and language models, it is difficult to learn using fractal images that do not include real-world concepts. Therefore, in this study, we are attempting to construct more realistic synthetic images from simulators that do not include issues such as privacy, copyright, and social bias using a simulator rather than fractals, and then use these to train vision-language models.
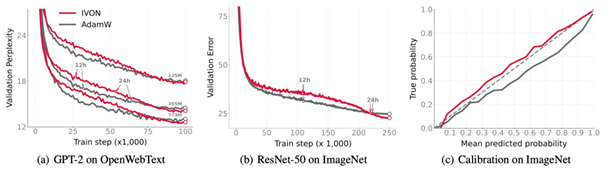
Improving the Reliability of LLMs Using Bayes Duality Theory
The reliability problem of LLMs, caused by hallucinations and attribution of the output, has not been solved. By using Bayes duality theory, it is possible not only to analyze the uncertainty of LLMs, but also to analyze how each training data affects the output. However, it has been thought that Bayesian deep learning, such as variational inference, would be difficult to apply to LLMs because the computational cost would be enormous even for small-scale models. Through joint research with RIKEN AIP, we developed a low-cost variational inference method called IVON, and applied it to LLMs for the first time.
Thesis 2023
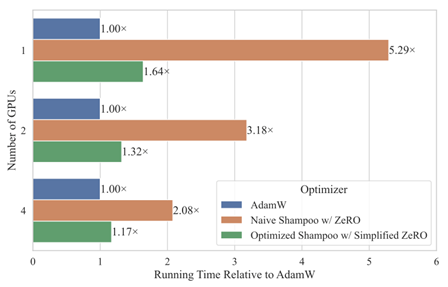
Development of Computationally Efficient Second-Order Optimizer for Large Language Models (Cong Bai)
In recent years, Large Language Models (LLMs) have garnered significant attention in the field of artificial intelligence due to their profound capabilities in understanding and generating natural language. However, the resource-intensive nature of training these huge models has led to monopolization by the tech giants, presenting a considerable bar- rier to progress within the field. Second-order optimizers, which leverage second-order information matrices such as Hessians, Fisher Information Matrices (FIMs) and gradient second moment matrices, hold promise for reducing the resources required for training by accelerating convergence. Yet, at the scale of deep learning, these second-order informa- tion matrices become impractically large. Although popular second-order optimizers like K-FAC and Shampoo have approximated these matrices, they still incur substantial over- head in language model training practice, forcing a compromise between tolerating this overhead and making further crude approximations, thereby hindering further research and application of them. This study aims at addressing this challenge and developing efficient second-order optimizers for training large language models.
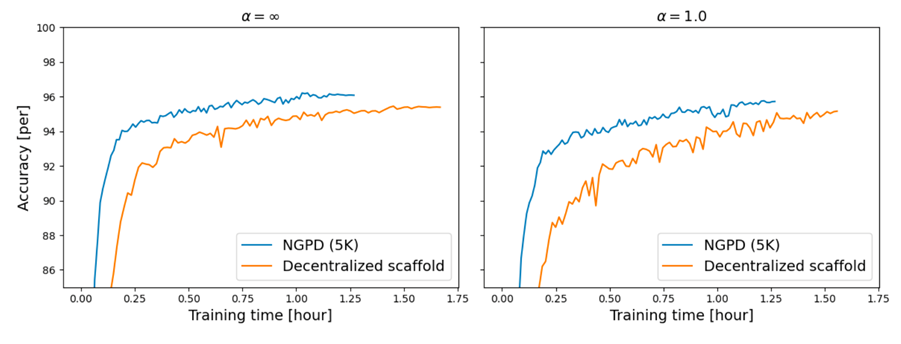
Distributed Learning Using the Natural Gradient Dual Method (Hiro Ishii)
In federated learning, a single model can be trained without collecting data from devices or servers, so even highly confidential data can be used for learning. In many cases, centralized federated learning is used, but distributed federated learning has also attracted attention in recent years due to its advantages of avoiding single points of failure and bottlenecks caused by the absence of a central server. However, the optimization method used in distributed cooperative learning is mainly a first-order optimization method that uses only the gradient, which results in excessive communication. In this study, we propose a new optimization method for distributed cooperative learning of deep neural networks, the Natural Gradient Primal Dual method (NGPD).
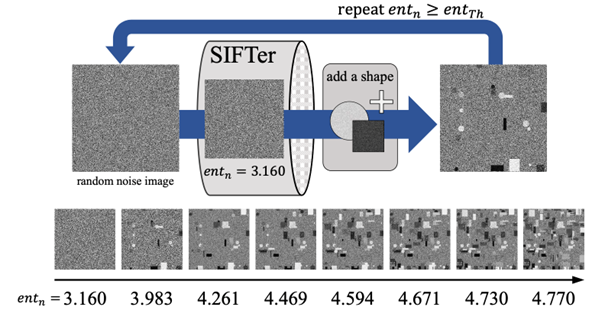
Pretraining of Vision Transformers Using Synthetic Images (Shota Nakamura)
As the size of the pretraining data sets for deep vision models continues to increase, it is becoming increasingly difficult to filter problematic images in terms of copyright, privacy, and ethics. In fact, in December 2023, LAION.ai was forced to take down LAION5B, a large-scale image-text dataset, due to the presence of inappropriate images in the dataset. One approach to avoiding such problems from the outset is to use synthetic image datasets, which are generated based on mathematical formulas and do not use real images, for some of the pre-training. The quality of synthetic images as a pre-training dataset can be continuously improved by changing the generation method, but existing approaches require many rounds of trial and error based on human knowledge, and are very labor-intensive. In this study, we designed an indicator to predict the “quality of the pre-training dataset”, and automatically constructed a synthetic image dataset that is highly effective for pretraining vision transformers.
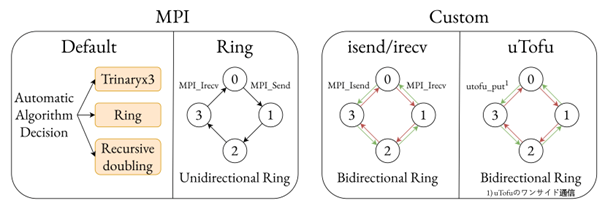
Accelerating Allreduce in Large-scale Parallel Training on Fugaku (Shukai Nakamura)
In training large-scale deep learning models, we use distributed training methods such as data parallelism to speed up the training and model parallelism to divide the model. When training deep learning models on the supercomputer “Fugaku”, although the performance per node is inferior to other GPU machines, a method is used to achieve speed improvement by training using the large-scale node configuration of “Fugaku” and large-scale parallelization. However, deep learning using large-scale parallelization has the drawback that the ratio of communication time to training time increases, and could slow down the training. The aim of this research is to accelerate AllReduce on Fugaku. Considering its application to deep learning models, we divided the 6-dimensional torus direct network of Fugaku into three dimensions in three different parallel methods, and developed an AllReduce algorithm that can be used in each of these divisions.
Acceleration of Diffusion Models Training and Sampling Through the Use of Multiple Models (Zhaoqing Wang)
In recent years, Diffusion Probabilistic Models (Diffusion Models or DPMs) have sparked a surge in generative models for images. However, diffusion models still face challenges in terms of training and sampling efficiency. While various efforts have been made to accelerate sampling or enhance training strategies, these improvements are constrained by the limitations of the single-model backbone used in diffusion models. After a thorough examination of the theoretical foundations and existing analyses, we propose two approaches to enhance the efficiency of training and sampling in diffusion models. Firstly, we advocate separating a denoising model and a score model from the diffusion model backbone, training them with specific targets using only one inference. Secondly, we suggest unfolding the single-model backbone into multiple individual models and training them in a distributed manner.
Bachelors Thesis 2023
Distributed Parallel Training of Large Language Models (Kazuki Fujii)
In recent years, various research institutions and companies have been developing large language models (LLMs). These models have attracted a great deal of attention for their ability to understand and generate language in a way that is similar to that of humans, and for their potential to be applied to a wide range of fields. Distributed parallel training is essential for the efficient training of large language models, and is an important factor that has a significant impact on training efficiency. However, in many cases, papers and technical reports mainly describe the performance of the model, the training corpus, and the model architecture, and the know-how regarding distributed parallel learning methods is not sufficiently shared. In addition, the optimal distributed training method depends greatly on the model size, model architecture, and training environment, and it is rare that the settings in a particular paper are optimal in all cases. In this study, we trained LLMs for multiple model sizes: 2.8B, 7B, 13B, 70B, and 175B. We pre-trained from scratch and also continually from a pre-trained model. We also trained a state space model, which is not a Transformer architecture.
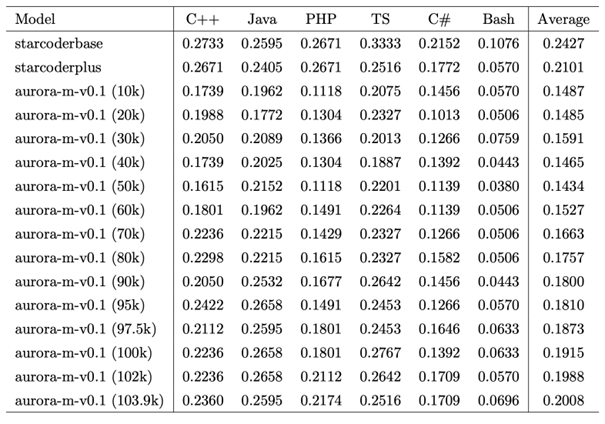
Development of a Multilingual Multiexpert Model Using Continuous Learning (Taishi Nakamura)
LLMs can solve many natural language processing tasks with 0-shot or few-shot learning by pre-training on large corpora without fine-tuning for each task. There is an increasing trend to develop LLM for non-English languages. There are still many challenges to develop models that can efficiently handle multiple languages and tasks. Despite the importance of learning to program in one's native language for non-English speakers, there are few models that support code generation in such languages. In this study, we developed a multilingual model by performing continuous pre-training using Japanese, English, Finnish, Vietnamese, Hindi, and code, based on starcoderplus, a model that was mainly trained using English and code.
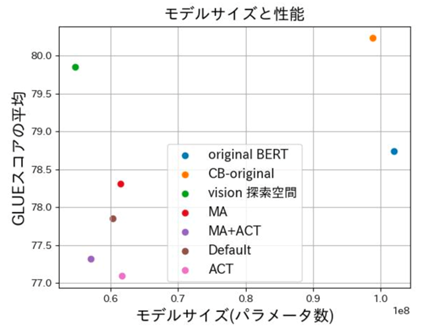
Architecture Search for Large-Scale Language Models (Takumi Okamoto)
BERT is a model that appeared in 2018 and achieved SOTA in 11 NLP tasks at the time. However, because BERT uses a large model size and a large amount of pre-training data sets to achieve high performance, it takes a long time to train. To solve this problem, we use model compression, which reduces the model size while maintaining or improving performance by reducing the number of parameters used in the model and the number of bits used to represent each parameter. The proposed methods for model compression include pruning, quantization, distillation, low-rank matrix approximation, and Neural Architecture Search (NAS). Of these methods, although various search methods and search spaces have been proposed for models of visual tasks, there are few proposals for BERT and GPT. Therefore, in this study, we conducted an experiment to reduce the model size by using NAS to search for the optimal structure in BERT.
Thesis 2022
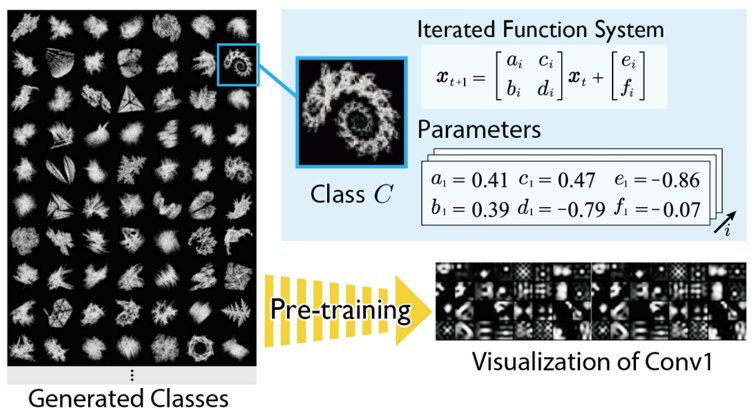
Scaling up Pre-training with Synthetic Images (Sora Takashima)
In the context of image recognition tasks, the highest accuracy has been achieved by ViT pre-trained on very large real image datasets such as JFT-300M/3B. On the other hand, labeled real image datasets used for pre-training have many problems such as ethical and copyright issues, difficulties in collection and labeling, and oligopoly by some organizations, and it is difficult to control these problems by increasing the dataset size. In this study, we developed three hypotheses about the human-made image dataset for FDSL to pre-training ViT: 1) contours of objects in the image are important, 2) variations in image representation are important, and 3) scaling up can improve the pre-training effect. We constructed new datasets {ExFractalDB, RCDB, VisualAtom} to test each hypothesis, and conducted a comparative verification of the pre-training effect of each dataset.
Model Reduction Effect of NAS during Finetuning of Vision Transformers (Xinyu Zhang)
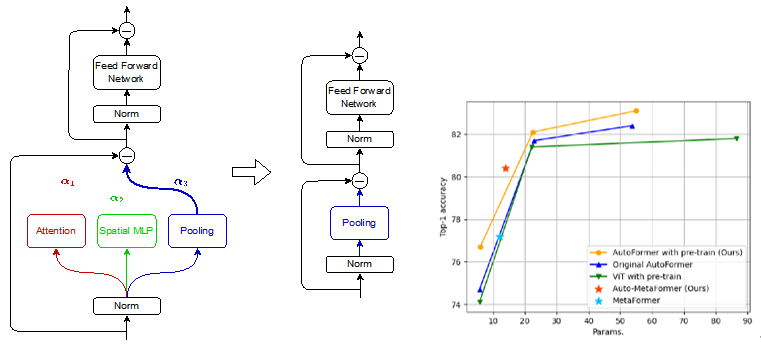
Vision Transformers (ViT), an application of Transformer used in natural language processing, have surpassed traditional Convolutional Neural Networks (CNN) in image classification on ImageNet by pre-training on large datasets. However, the models are becoming so large to achieve high accuracy that they cannot even fit on a single GPU, which limits their usefulness during inference. In order to reduce the size of such large ViT models while keeping their performance, we utilize Neural Architecture Search (NAS), which makes it possible to automatically design architectures of deep neural networks. We propose a method called Auto-MetaFormer, which can automatically search for architecture of MetaFormer based on algorithm of DARTS by Liu et al. It uses a gradient based approach to search for architecture by training architecture weights along with model weights. Auto-MetaFormer succeeds in automatically searching the MetaFormer architecture, gaining a 2% increase in accuracy using the same number of parameters. For the same classification accuracy, the number of parameters also be further reduced by 20% compared to the manually designed architecture.
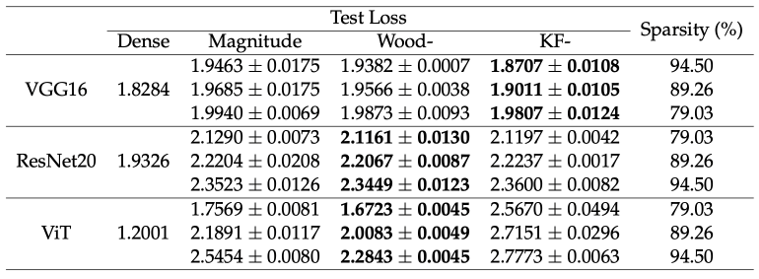
Neural Network Pruning based on Second-Order Information (Sixue Wang)
Nowadays, deep learning has demonstrated its ability to solve arduous tasks in different domains, such as computer vision, voice interaction, and natural language processing, but there is a huge gap between academia and industry when considering cost, efficiency and quality. Neural network pruning is a common technique to reduce the size of neural networks. It selects some redundant parameters and removes them all. The goal of this thesis is to exploit second-order information in neural network pruning in a practical manner. We demonstrate that second-order neural network pruning can achieve better or comparable results within similar computational resources.
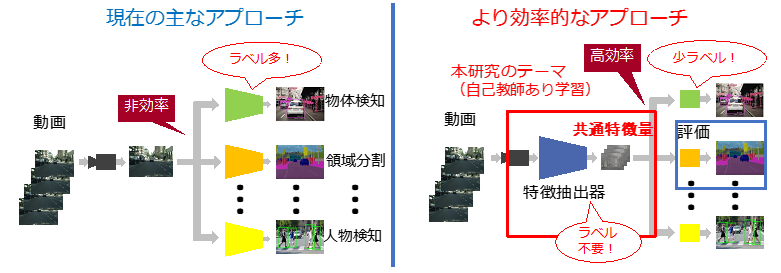
Large-Scale Self-Supervised Learning of Driving Videos (Tomoya Takahashi)
In automated driving, recognition of the external environment obtained from cameras and lidar is the core of technology to ensure safety. Although the accuracy of these recognitions has been dramatically improved with the advent of deep learning, it is still not sufficient to realize fully automated driving. One of the reasons for this is that while a huge amount of vehicle driving data can be collected, the annotation cost of true-value labels is high, and it is difficult to prepare enough teacher data for learning. In this study, we aim to construct a recognition model that is robust to temporal changes in the visibility of objects by pre-training running videos using self-supervised learning on a pixel-by-pixel basis and by using optical flow. As a downstream task to evaluate the effect of the pre-training, we evaluated semantic segmentation using CityScapes. As a result, we found that accuracy varied greatly depending on the definition of neighborhood when comparing image pixels. In addition, we found that the accuracy can be further improved by using a mask to remove false positive examples, in which a pixel pair that is not originally a positive example is judged to be a positive example.
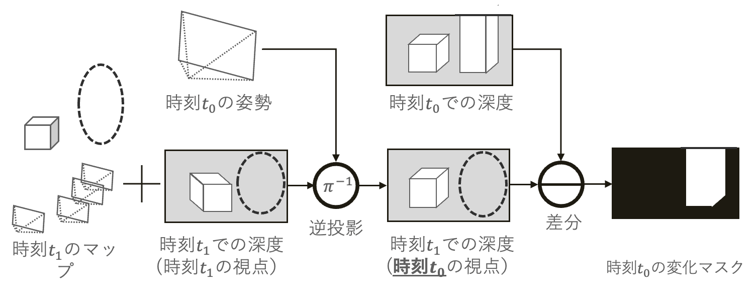
Change Detection by Visual SLAM Using Deep Learning (Kai Okawa)
Visual SLAM, which estimates the camera's self-position and reconstructs a 3D map of the surrounding area from a sequence of images, is one of the most important fundamental technologies in an AI society, playing the role of "eyes" in automated driving, AR/MR, and robotics. In recent years, methods capable of robustly estimating self-position and 3D maps in real time have emerged in Visual SLAM research. In addition, methods incorporating deep learning, which has evolved remarkably in recent years, have been proposed, enabling more accurate self-position estimation and 3D map restoration. However, after a certain period of time has passed since the 3D map was created, the actual scene may change, and discrepancies may arise between the 3D map and the actual scene. Such discrepancies degrade the accuracy of Visual SLAM and cause the 3D map to become bloated due to the accumulation of old information. In this study, we propose a change detection method for 3D maps at two different times, using information obtained from DROID-SLAM, which estimates a change mask using the dense depth information estimated by DROID-SLAM and the optical flow estimated by a regression-type neural network. In addition, a new change-aware objective function is introduced to optimize the change mask. Furthermore, a synthetic image dataset suitable for this study was created, and experiments were conducted. Through the experiments, we confirmed that it is possible to estimate the change mask for the two-time 3D map estimated by DROID-SLAM.
Bachelors Thesis 2022
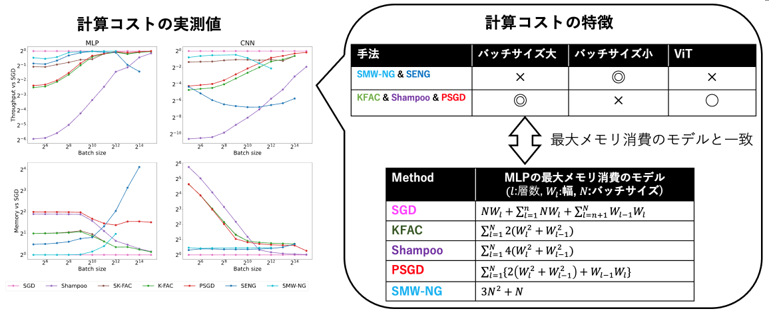
Gradient Preconditioning in Second-Order Optimization of Deep Learning (Satoki Ishikawa)
Gradient preconditioning using curvature matrices (Hessian matrix, Fisher information matrix, second-order moments) has become an important technique in a wide range of deep learning tasks. Gradient preconditioning is used in various domains, including second-order optimization to speed up deep learning optimization, continuous learning, branch-and-bound pruning, and Bayesian inference. In second-order optimization of deep learning, gradient preconditioning is performed after approximating the curvature matrix. Various types of approximation algorithms have been proposed for this purpose, but the differences in their characteristics have rarely been investigated. Therefore, this study compares these algorithms from two perspectives: computational aspects such as memory consumption and computation time, and training convergence. Since the overall learning time is determined by the product of the computation time per step and the number of steps required for convergence, it is very important to examine both of these characteristics. The results show that many second-order optimization methods, such as KFAC and Shampoo, have the potential to be particularly useful for learning at large batch sizes. We also found that second-order optimization methods such as SENG and SMW-NG, which use the SMW formula for the inverse matrix computation, have different properties than other methods.
Pre-training of Vision Transformers Using Newton Fractals (Toshiki Omi)
In the field of image recognition, the mainstream method is to use a large-scale natural image dataset such as JFT-300M/3B for pre-training, followed by fine-tuning with the data of the target task. It is known that the larger the dataset used for pre-training, the higher the image classification and object recognition performance can be obtained, making the choice of which dataset to use for pre-training an important issue. However, natural image datasets pose many problems, including the collection of large numbers of images, labeling costs, copyright issues, content bias issues, and issues of fairness and offensive labels. In this study, we pre-trained the Vision Transformer Tiny model using an image dataset consisting of Newton Fractal images generated by the Newton method, and evaluated the performance of the dataset by the accuracy of the fine tuning task of CIFAR-10/100. The performance of the dataset was evaluated by the accuracy of CIFAR-10/100 fine tuning task. In addition, we conducted similar experiments on FractalDB and ExFractalDB, which are the conventional fractal datasets, and ImageNet, which is a natural image dataset, to compare the performance of the conventional method. As a result, the pre-training effect of the Newton Fractal image dataset was confirmed. As with the conventional FDSL dataset, the performance of the dataset consisting of black-and-white images was higher than that of color or grayscale images, and the performance was improved by changing the image generation conditions. Although the pre-training effect was lower than that of ImageNet, the pre-training effect was higher than that of the image representations used in conventional FDSL methods.
Accelerating Quantum Vortex Simulations with Fast Multipole Methods (Tomokazu Saito)
Fluids at cryogenic temperatures have zero viscosity due to quantum effects. Such fluids are called superfluids. The physical properties of superfluids are important from an engineering viewpoint, but for applications, it is necessary to elucidate complex phenomena such as turbulence in superfluids. However, experiments on superfluids require expensive equipment because the fluid must be maintained at extremely low temperatures. Therefore, it is important to analyze the behavior of turbulence by simulation. However, methods that require a very fine mesh, such as the finite element method, require an enormous amount of time. Quantum turbulence is am inviscid fluid consisting of many vortex threads, and it is effective to use the Vortex Method. In this study, FMM, which calculates the interaction between vortex particles based on the Biot-Savart law, was implemented on CPUs and GPUs, and its calculation speed and accuracy were evaluated. However, we were able to confirm that the error decreases with increasing P in the implementation. Furthermore, we confirmed that the error converges to a constant value around 274 periodic images when the number of particles is 104 and the order of FMM is P = 10, while FMM can calculate periodic boundary conditions with minimum overhead.
Thesis 2021
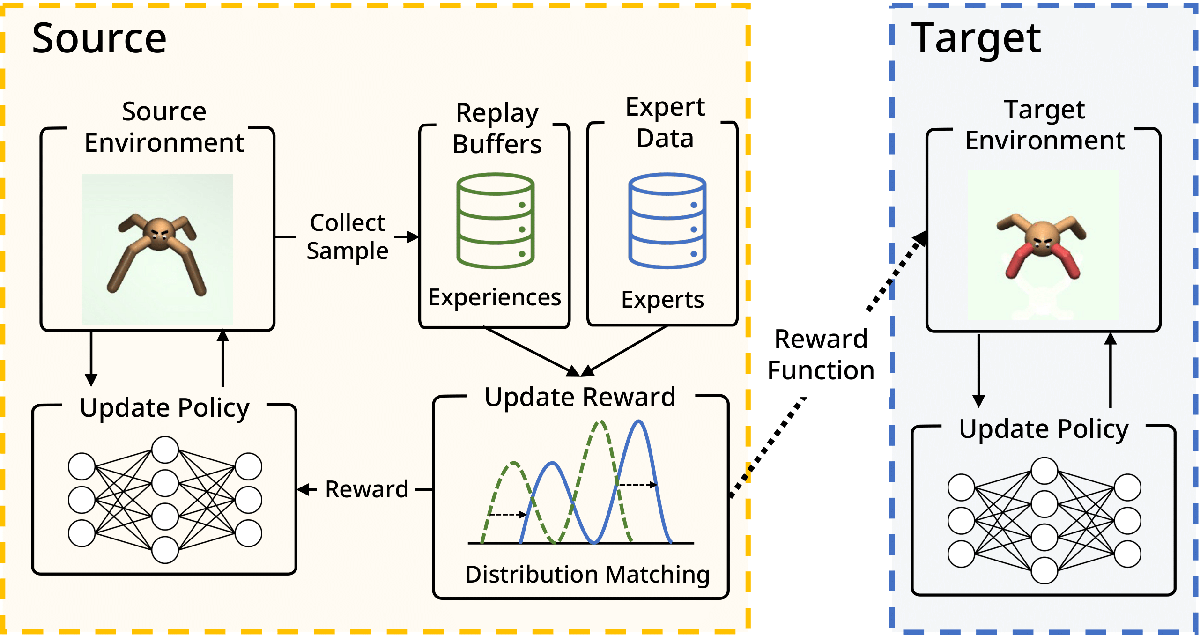
Off-Policy Inverse Reinforcement Learning via Distribution Matching (Hana Hoshino)
Inverse Reinforcement Learning (IRL) is attractive in scenarios where reward engineering can be tedious. However, prior IRL algorithms use on-policy transitions, which require intensive sampling from the current policy for stable and optimal performance. This limits IRL applications in the real world, where environment interactions can become highly expensive. To tackle this problem, we present Off-Policy Inverse Reinforcement Learning (OPIRL), which (1) adopts off-policy data distribution instead of on-policy and enables significant reduction of the number of interactions with the environment, (2) learns a reward function that is transferable with high generalization capabilities on changing dynamics, and (3) leverages mode-covering behavior for faster convergence. We demonstrate that our method is considerably more sample efficient and generalizes to novel environments through the experiments. Our method achieves better or comparable results on policy performance baselines with significantly fewer interactions. Furthermore, we empirically show that the recovered reward function generalizes to different tasks where prior arts are prone to fail.
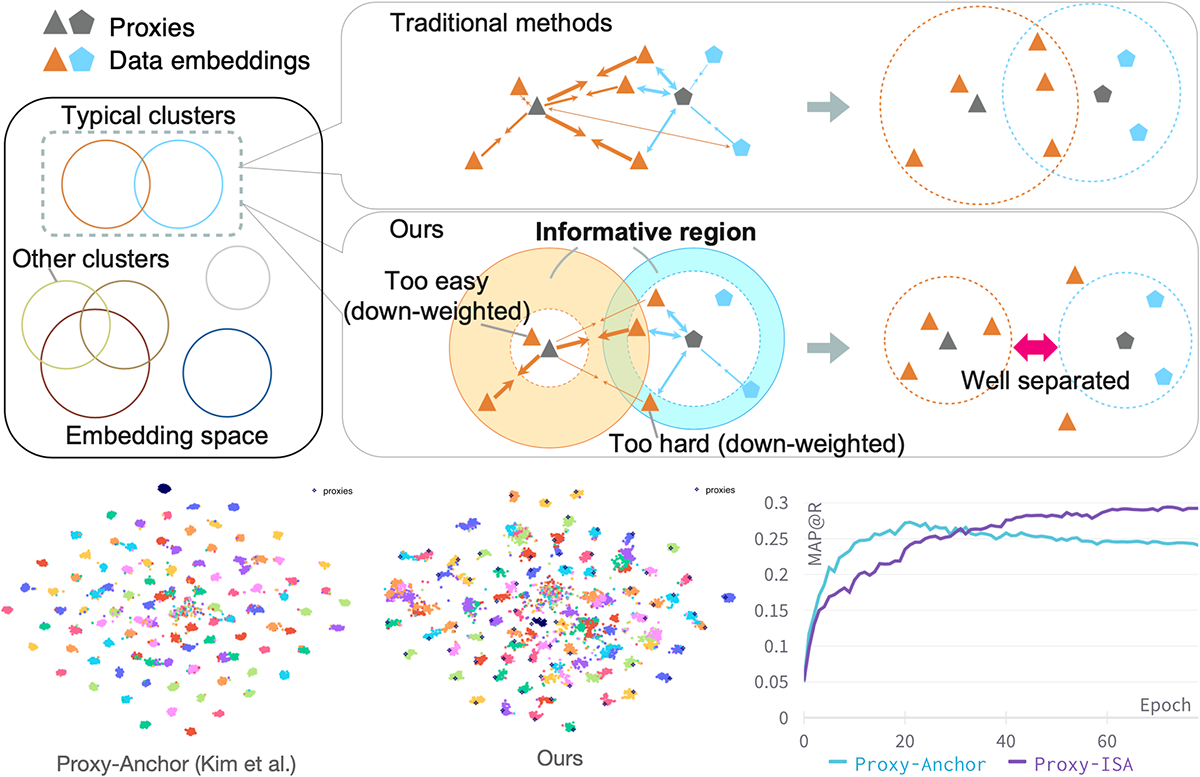
Informative Sample-Aware Proxy for Deep Metric Learning (Aoyu Li)
Metric Learning is one if the core fundamental tasks of machine learning. In deep metric learning (DML), the proxy-based methods are drawing more and more attention recently because of their flexibility and efficiency while maintaining higher performance. In this work, we propose a novel proxy-based method combined with class-dependent dynamic weighting, called Informative Sample-Aware Proxy (Proxy-ISA).
Proxies, which are class-representative points in the representation space, receive updates based on proxy-sample similarities as sample representations do. In existing methods, it may be possible that a relatively small number of samples producing large gradient magnitudes (i.e., hard samples) and a relatively large number of samples producing small gradient magnitudes (i.e., easy samples) play a major part in the update. Based on the assumption that acquiring too much sensitivities to such extreme sets of samples would deteriorate the generalization ability, the proposed Proxy-ISA directly modifies a gradient weighting factor to each sample. In this work, we first design a method to estimate the learned class-related region to acquire the information of class hardness. By defining the hard and easy samples adaptively to the class hardness, each proxy identifies its own hard and easy samples and reduces their weighting factors with a scheduled threshold function, so that the model acquires more sensitivity to the intermediate samples, which is called "informative" samples. Furthermore, we incorporate the idea of active learning to emphasize the informative samples dynamically according to the learning step, and the dynamic weights are assigned separately for positive pairs and negative pairs. Extensive experiments on the CUB-200-2011, Cars-196, Stanford Online Products and In-shop Clothes Retrieval datasets demonstrate superiority of Proxy-ISA over the state-of-the-art methods.
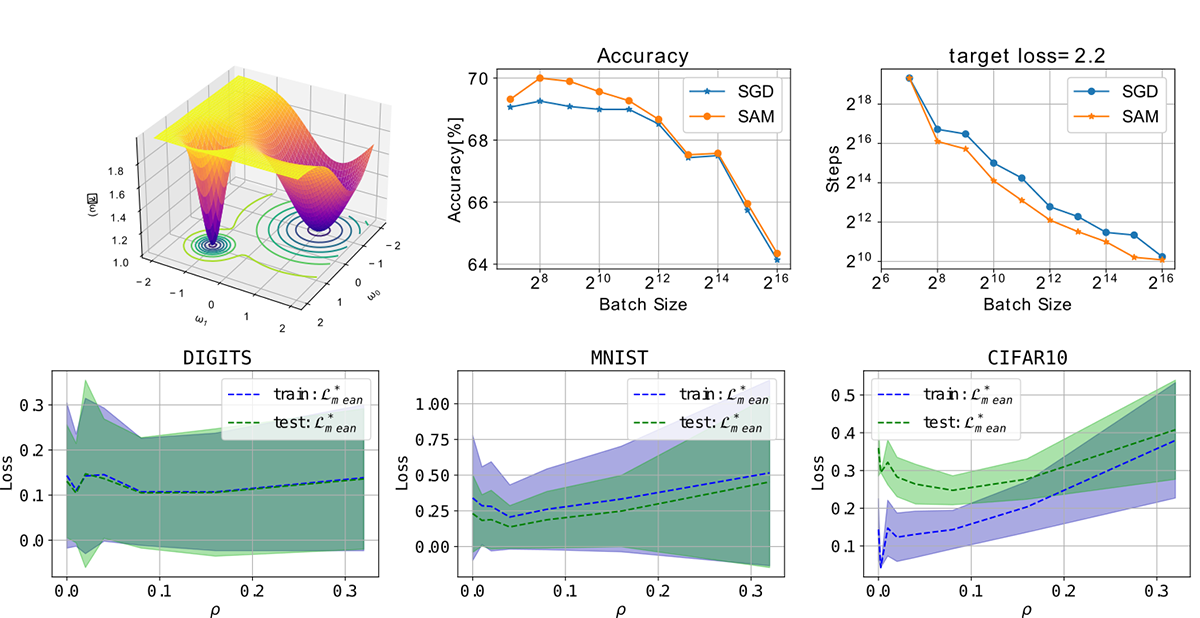
On the generalization gap of SAM optimizers for very large batch sizes (Elvin Munoz)
The generalization properties of a trained network are highly tied to the geometrical shape of the loss function evaluated at the parameters of the model; it has been found that flat minima increase the generalization properties of a neural network. Due to the stochasticity of most optimizers such as SGD, normally a flat minima will be found rather than a sharp minima. However, as we increase the batch size and thus reduce the stochasticity of the training process, it becomes more likely to fall into a sharp minima. There have been many methods that have been devised to counteract this effect and obtain high generalization properties even when using large batches, one of such methods is SAM (Sharpness-aware minimization). This method has been proven to improve the generalization properties of trained neural networks in the small-mid range of batch sizes and even it has been found to work in distributed training. However, a more in-detail study of its capabilities at higher batch sizes is needed; moreover this method introduces a new hyperparameter (neighborhood size) that needs to be tuned. The main goal of this work was to shed some light at the behavior of this optimizer when using a large batch (reaching almost full batch) and a study of the behavior of the neighborhood size for proper tuning.
Thesis 2020
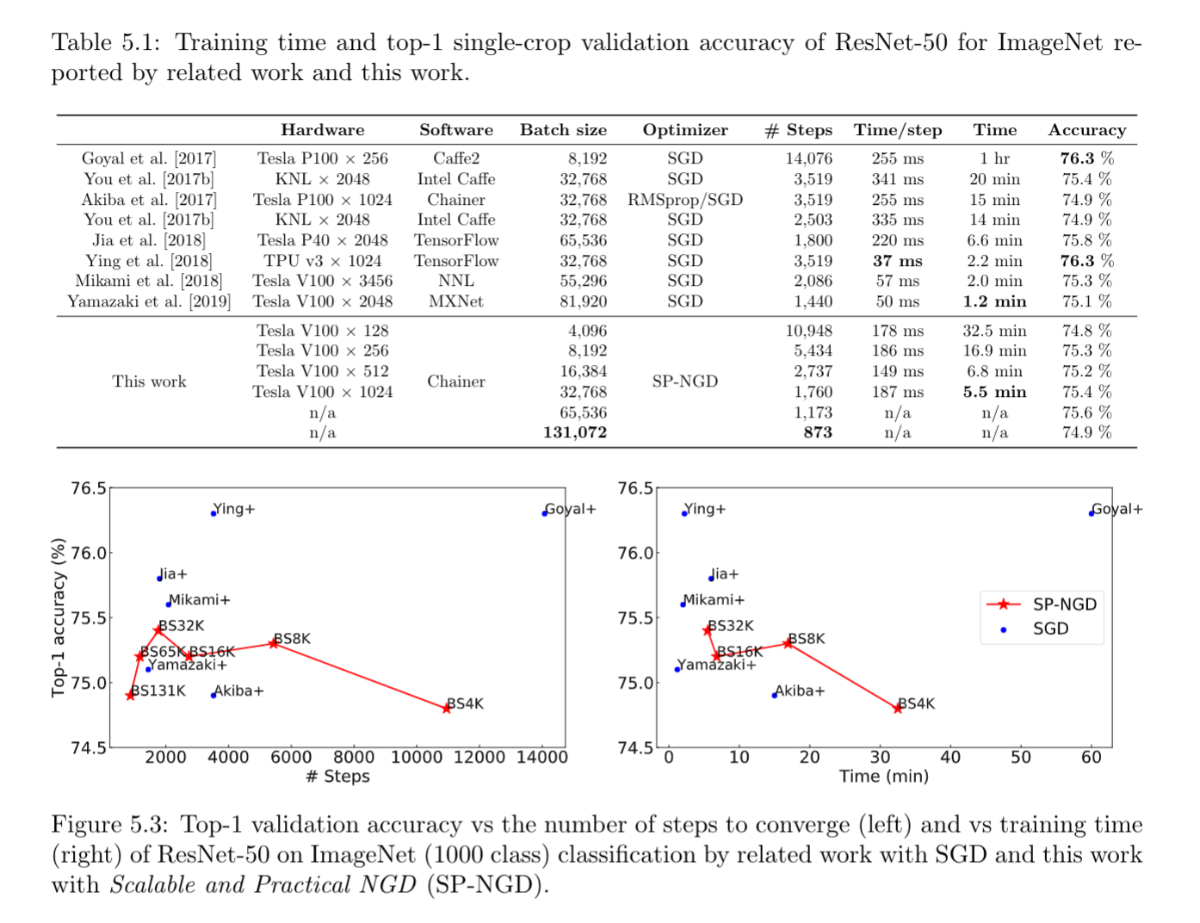
Second-order Optimization for Large-scale Deep Learning(Kazuki Osawa)
Large-scale distributed training of deep neural networks results in models with worse generalization performance as a result of the increase in the effective mini-batch size. Previous approaches attempt to address this problem by varying the learning rate and batch size over epochs and layers, or ad hoc modifications of Batch Normalization. We propose Scalable and Practical Natural Gradient Descent , a principled approach for training models that allows them to attain similar generalization performance to models trained with first-order optimization methods, but with accelerated convergence. Furthermore, SP-NGD scales to large mini-batch sizes with a negligible computational overhead as compared to first-order methods. We evaluate SP-NGD on a benchmark task where highly optimized first-order methods are available as references: training a ResNet-50 model for image classification on the ImageNet dataset. We demonstrate convergence to a top-1 validation accuracy of 75.4% in 5.5 minutes using a mini-batch size of 32,768 with 1,024 GPUs, as well as an accuracy of 74.9% with an extremely large mini-batch size of 131,072 in 873 steps of SP-NGD.
Thesis 2019
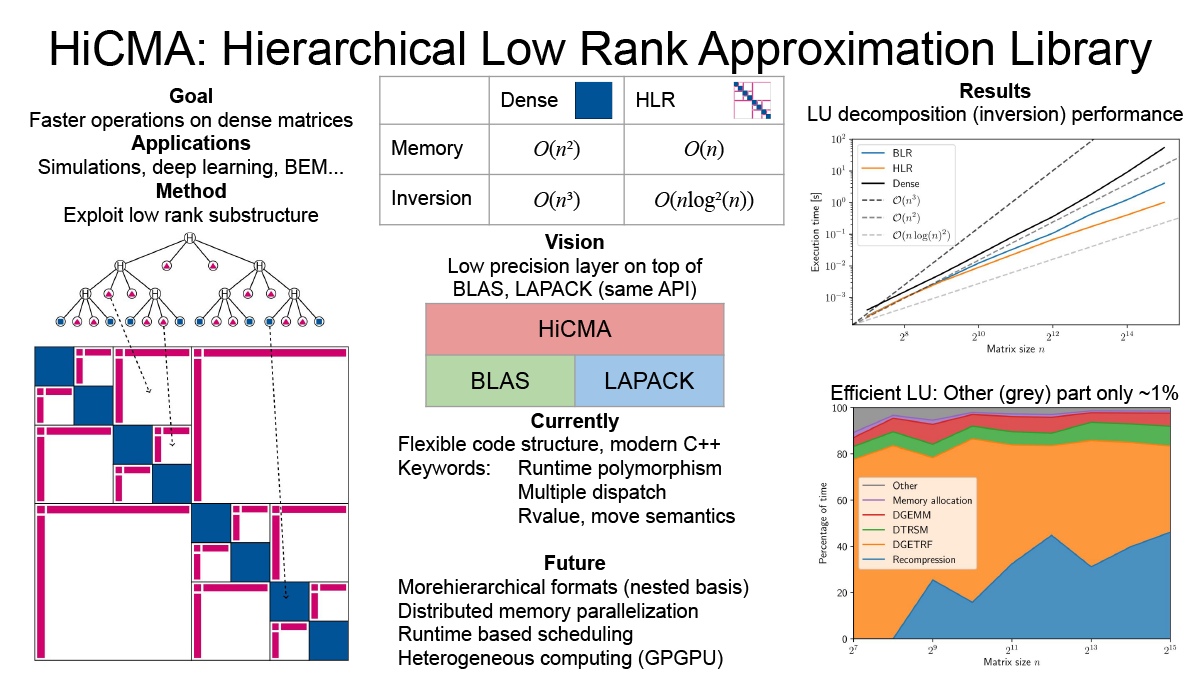
Efficient library for hierarchical low rank approximation (Peter Spalthoff)
Dense matrices have a quadratic memory complexity and many operations on them have cubic scaling. This makes them prohibitively expensive for large scale operations. In many applications (covariance matrices, BEM...) a substructure of low rank blocks is found. This substructure can be exploited to create an efficient compression of the matrix, called hierarchical low rank approximation. On the resulting so-called Hierarchical Matrices, which only have linear storage complexity, all arithmetic operations (multiplication, inversion...) can be defined. These operations are also much faster with cloes to linear complexity. We are working on a modern, flexible library with distributed memory parallelization on heterogeneous nodes.
Thesis 2018
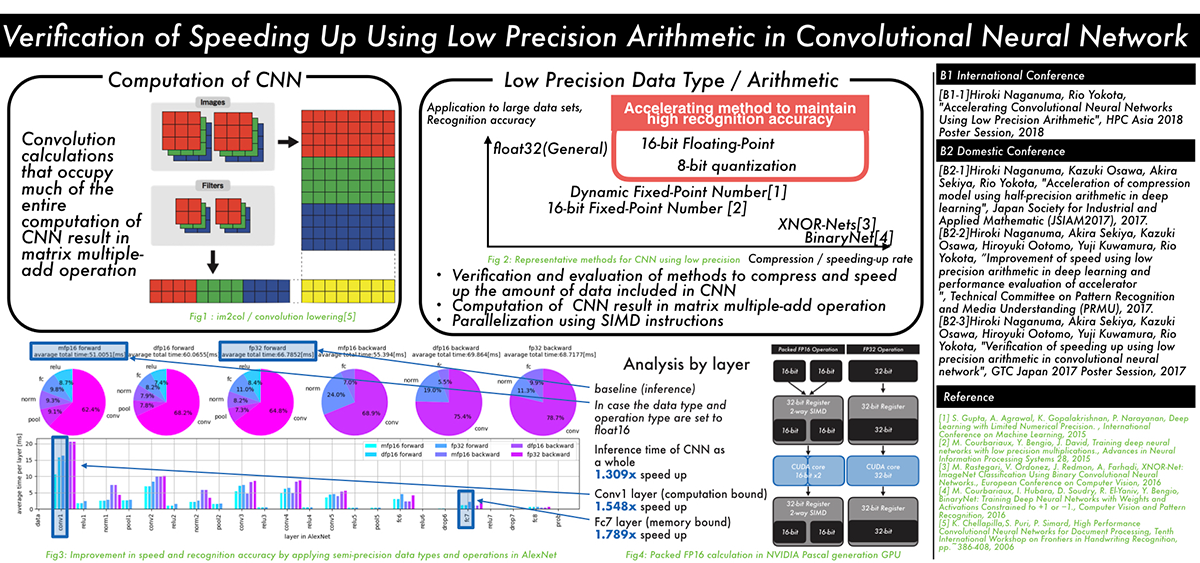
Verification of speeding up using low precision arithmetic in convolutional neural network (Hiroki Naganuma)
The recent trend in convolutional neural networks (CNN) is to have deeper multilayered structures. While this improves the accuracy of the model, the amount of computation and the amount of data involved in learning and inference increases. In order to solve this problem, several techniques have been proposed to reduce the amount of data and the amount of computation by lowering the numerical precision of computation and data by utilizing the CNN's resistance to noise.
However, there is a lack of discussion on the relationship between parameter compression and speedup within each layer of the CNN.
In this research, we propose a method to speed up the inference by using half precision floating point SIMD instructions, by applying low precision to the learned model, in addition to reducing the data of the CNN model, and speeding up data access for layers that are computation-bound.
We examined the influence of CNN recognition accuracy, the speedup for each layer, and its reason, when we apply our method.
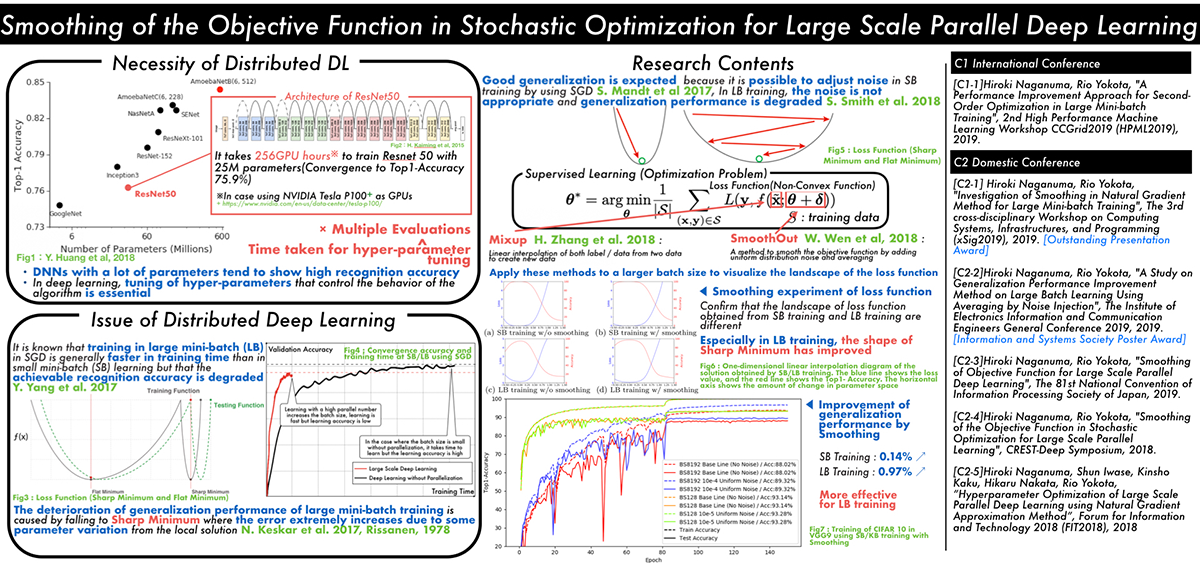
Smoothing of the Objective Function in Stochastic Optimization for Large Scale Parallel Deep Learning (Hiroki Naganuma)
Classical learning theory states that when the number of parameters of the model is too large compared to the data, the model will overfit and the generalization performance deteriorates. However, it has been empirically shown that deep neural networks (DNN) can achieve high generalization capability by training with extremely large amount of data and model parameters, which exceeds the predictions of classical learning theory. One drawback of this is that training of DNN requires enormous calculation time. Therefore, it is necessary to reduce the training time through large scale parallelization. Straightforward data-parallelization of DNN degrades convergence and generalization. In the present work, we investigate the possibility of using second order methods to solve this generalization gap in large-batch training. This is motivated by our observation that each mini-batch becomes more statistically stable, and thus the effect of considering the curvature plays a more important role in large-batch training. We have also found that naively adapting the natural gradient method causes the generalization performance to deteriorate further due to the lack of regularization capability. We propose an improved second order method by smoothing the loss function, which allows second order methods to generalize as well as mini-batch SGD.